
XVIIe siècle : Römer
Caractéristiques et généralités sur les satellites galiléens de Jupiter:
les satellites galiléens de Jupiter sont des corps remarquables à bien des égards. Ce sont les premiers astres connus non visibles directement à l’œil nu. Ils ont des tailles semblables à Mercure et forment, en tournant autour de Jupiter, un système solaire en miniature où la plupart des problèmes de la mécanique céleste sont rassemblés : perturbations par l’aplatissement de Jupiter, par le Soleil, par Saturne et perturbations relatives aux mouvements rapides sont facilement observables et génèrent des phénomènes d’éclipses spectaculaires. Les satellites galiléens se distinguent des autres satellites de Jupiter qui ne sont que des petits corps semblables à des astéroïdes communs. Les sondes spatiales nous ont récemment montré que ces corps étaient d’une diversité géologique intéressante (volcans actifs , présence de glace...).

 |
La figure ci-contre montre les tailles comparées des satellites de Jupiter avec la lune, Mercure, Mars et Pluton. On voit qu'il s'agit bien de véritables petites planètes. Le plus gros astéroïde a un diamètre qui n'atteint qu'un quart du plus petit satellite galiléen. |
Les satellites de Jupiter (Io, Callisto, Ganymède et Europe), leurs éclipses et la vitesse de la lumière :
Les astronomes, par leurs observations, ont montré l’intérêt et la qualité de la méthode de détermination de la longitude fondée sur les éclipses des satellites de Jupiter. Les voyageurs, marins, jésuites... formés à l’Observatoire de Paris vont pouvoir, des pays lointains où ils se rendent, envoyer leurs déterminations tant en latitude qu’en longitude.
Cassini I ( Giovanni-Dominico , plus tard Jean-Dominique ) astronome italien appelé par Colbert pour diriger l’Observatoire de Paris , établira, dans la rotonde Ouest de l’Observatoire, un « parterre géographique » qui en couvre toute la surface. Tracé à l’encre, il est corrigé chaque fois qu’une valeur nouvelle parvient à Paris ; devenu obsolète et demeuré fragile par sa nature même, il finira par disparaître.
Pour mener à bien de telles observations, il est nécessaire de disposer de bonnes prédictions des phénomènes. Cassini I constate bientôt que les Tables des satellites de Jupiter présentent des écarts de temps qui atteignent la dizaine de minutes en plus ou en moins par rapport aux observations. Et ce notamment pour le satellite le plus proche de la planète, celui dont les éclipses sont les plus fréquentes. C’est aussi celui, plus tard appelé Io, qui a été le plus fréquemment observé.
Les satellites de Jupiter et la découverte de Römer :
 |
L’astronome danois Olaüs Römer travaillait à l’observatoire de Paris, appelé par Cassini I , pour étudier les mouvements des satellites de Jupiter , il observa que la vitesse de la lumière n’était pas infinie grâce à l’observation des éclipses des satellites de Jupiter (en particulier Io). |
En principe, l’intervalle de temps qui sépare deux éclipses devait être constant lors d’une révolution de Io autour de Jupiter , soit 42,5h.
Or Römer observa que cela n’était vrai que lorsque Jupiter était proche de nous (distance Terre-Jupiter constante) mais que les immersions successives prenaient de plus en plus de retard (par rapport à des intervalles constants) au fur et à mesure que la Terre s’èloigne de Jupiter, le cumul des retards atteignant 16 minutes entre une opposition et la conjonction suivante.
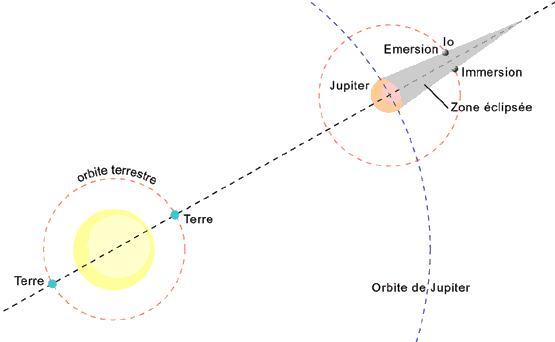
RÖMER COMPRIT QU’IL FALLAIT TENIR COMPTE DU TEMPS DE PARCOURS DE LA LUMIERE POUR ALLER DE IO A LA TERRE.
Nous allons donc vous expliquer sa méthode d’observation, ainsi que ses calculs :
| Prenons comme origine des dates t = 0, l’instant où la Terre se trouve en L et où on observe l’immersion de Io. A quelle date devrait-on apercevoir l’immersion suivante, la Terre se trouvant en K (elle a bougé) si la lumière était instantanée ? Le temps qu’a mis Io pour faire une révolution, soit 42,5h. En réalité le temps de révolution était augmenté du temps t’ mis par la lumière pour parcourir la distance LK le rayon de l’orbite R de la terre autour du soleil permet de calculer LK et par là même occasion de calculer  |
 |
Calculons maintenant la distance Terre Jupiter :
A l’opposition (lorsque Jupiter la Terre et le Soleil sont alignés figure 1),
l’observation de Jupiter est facile, la première éclipse avant l’opposition a lieu plus tôt.
| On a : TS = 1 U.A. et TJ = 5,2 – 1 = 4,2 U.A. = D1 |
A la conjonction (Jupiter, Soleil, Terre sont alignés dans cet ordre figure 2),
on ne peut pas observer Jupiter depuis la Terre.
L’observation n’a lieu que, par exemple, 261 jours après l’opposition.
L’angle a qui sépare les rayons issus du Soleil vers les 2 planètes est grand :
| JST = 360 - a |
Dans le triangle quelconque JST, la relation d’ALKASHI (Extension de Pythagore) s’écrit :
| JT² = JS² + ST² - 2(JS x ST) x Cos (360-a) | |
| avec D2 = JT soit : D2 = 5,2² +1²-2(5,2x1) x Cos (360-a) |
|
| Or a = aT - aJ où aT = 261,17° est l’angle « balayé » par la Terre et aJ l’angle « balayé » par Jupiter pendant la même durée |
|
| aJ = (261 / 4332,5 ) x 360° = 21,68°, la période de Jupiter valant 4332,5 de nos jours. |
|
Le calcul conduit à (D2)² = 33,32 |
Le trajet de la lumière apparaît plus long sur la figure 3 qu’en 1 et l’on a D2 – D1 = 1, 57 U.A.
Comme la durée supplémentaire est de l’ordre de 16 minutes, la vitesse de la lumière vaut :

 |
 |
 |
||
| Figure 1 : Jupiter en opposition : D1 = 4,2 UA .La dernière éclipse de IO a été observée quelques jours avant |
Figure 2 : Jupiter en conjonction n’est pas observable depuis la Terre. |
Figure 3 : Jupiter est à nouveau observable. Première éclipse après la conjonction. On connaît l’angle JST, on en déduit ST = D2. |
Les valeurs utilisées pour ce calcul sont tirées d’une expérience réalisée en 1960 : la valeur de la vitesse de la lumière sera donc, comme le disait Römer, un ordre de grandeur.
Son expérience comportait plusieurs sources d’erreurs, ce qui explique la différence de cette valeur avec la valeur actuelle :
- La limite de l’ombre de Jupiter n’est pas nette et la taille de Io n’étant pas négligeable, il n’apparaît pas et ne disparaît pas instantanément.
- Il est difficile de suivre Jupiter sur un an.
- L’éclipse de Io ne se produit pas toujours au niveau de l’équateur Jovien, sa durée est donc variable.
- Io est très proche de Jupiter, les forces de gravité qu’elle subit, perturbent son orbite.
Avec la valeur de l’unité astronomique estimée par Cassini I, Römer trouva une valeur de la vitesse de la lumière égale à 213 000 km/s. Actuellement il aurait trouvé 298 000 km/s. Avec l’expérience de 1960 on trouve 244 658 km/s. |